Answer:

Explanation:
Assuming that the tree is perpendicular with the ground, we can use trigonometric ratios to find the height of the tree.
First, let's draw a diagram. From the point on the ground to the base, it is 120 feet and forms a 30 degree angle. We want to find the height of the tree, which is labeled h. (The diagram is attached and not to scale).
Next, recall the ratios.
- sin(θ)= opposite/hypotenuse
- cos(θ)= adjacent/hypotenuse
- tan(θ)= opposite/adjacent
We see that the height is opposite the 30 degree angle and 120 is adjacent.
Since we are given opposite and adjacent, we must use tangent.
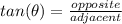
Substitute the values in.
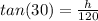
We are solving for h, so we must isolate it. It is being divided by 120 and the inverse of division is multiplication. Multiply both sides by 120.

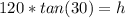
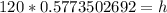
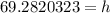
Round to the hundredth place (2 decimal places). The 2 in the thousandth place tells us to leave the 8 in the hundredth place.
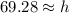
The height of the tree is about 69.28 feet.