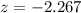Question

Decide whether the normal sampling distribution can be used. If it can be​ used, test the claim about the population proportion p at the given level of significance alpha using the given sample statistics. Claim: p is not equal to 0.22; Alpha = 0.01; Sample​ statistics: ​p = 0.15, n = 180Can the normal sampling distribution be​ used? A. ​No, because np is less than 5. B. ​No, because nq is less than 5. C. ​Yes, because both np and nq are greater than or equal to 5. D. ​Yes, because pq is greater than alpha = 0.01. State the null and alternative hypotheses. Determine the critical value(s).Find the z-test statistic.

Answer 1

A

The correct option is C

B

The value of z-test is
`z = -2.267`

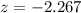
Explanation:

From the question we are told that

The null hypothesis
`H_o : p = 0.22`

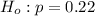
The alternative hypothesis
`H_a : p \\e 0.22`

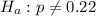
The level of significance is
`\alpha = 0.01`

The sample proportion is
`\^ p = 0.15`

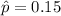
The sample size is n = 180

Generally from central limit theorem

if np and nq are > 5 then normal sampling distribution can be used

So

np = 180 * 0.22 = 39.6 > 5

and

nq = 180 * (1 -0.22) = 140.4 > 5

So normal sampling distribution can be used

Generally the z-test is mathematically represented as

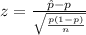
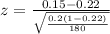
`z = \frac{\^ p - p }{ \sqrt{( p(1- p ) )/(n ) } }`

=>
`z = \frac{ 0.15 - 0.22 }{ \sqrt{( 0.2(1- 0.22 ) )/( 180 ) } }`

=>
`z = -2.267`