Question

Recently, a new drug has been announced that claims to make Hulks less angry. The company claims that it will benefit those who take it. To defend their claim, a research group put together a control and test group, one with a placebo and the other with the drug. Each group was made up of 150 Hulks. 78 of them reported an improvement from the placebo group, while 96 reported improvement from the drug group. (a) Conduct an appropriate test at a = 0.05 to determine if any differences exist between the drug group and placebo group. Show all your work, and state your conclusion. (b) Conduct another appropriate test (a different type of test) at a = 0.05 to determine if any differences exist between the drug group and placebo group (if they are distributed the same way). Show all your work, and state your conclusion.

Answer 1

orange 9,87

Explanation:

Answer 2

Test statistic

|Z| = 2.105632 > 1.96 at 0.05 level of significance

Null hypothesis is rejected at 0.05 level of significance

There is difference exist between the drug group and placebo group

Explanation:

Step(i):-

Given each group was made up of 150 Hulks. 78 of them reported an improvement from the placebo group.

first sample proportion

`p^(-) _(1) = (78)/(150) = 0.52`

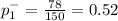
Second sample proportion

`p^(-) _(2) = (96)/(150) = 0.64`

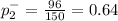
a) Null Hypothesis : H₀ : There is no difference exist between the drug group and placebo group

H₀ : p₁ = p₂

Alternative Hypothesis : H₁ : There is difference exist between the drug group and placebo group

H₀ : p₁ ≠ p₂

b)

Step(ii):-

`Z = \frac{p_(1) -p_(2) }{\sqrt{PQ((1)/(n_(1) ) +(1)/(n_(2) ) }) }`

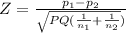
where

`P = (n_(1) p^(-) _(1) + n_(2) p^(-) _(2) )/(n_(1)+n_(2) )`

`P = (150 X 0.52+ 150 X 0.64)/(150+150 )`

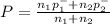
P = 0.58

Q = 1- P = 1- 0.58 = 0.42

`Z = \frac{p_(1) -p_(2) }{\sqrt{PQ((1)/(n_(1) ) +(1)/(n_(2) ) }) }`

`Z = \frac{0.52 -0.64}{\sqrt{0.58 X 0.42((1)/(150 ) +(1)/(150 ) }) }`

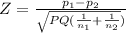
Z = -2.105632

|Z| = |-2.105632| = 2.105632

Level of significance = 0.05

Z₀.₀₅ = 1.96

Final answer:-

|Z| = 2.105632 > 1.96 at 0.05 level of significance

Null hypothesis is rejected at 0.05 level of significance

There is difference exist between the drug group and placebo group