Question

A quantity of hot water at 91°C and another cold one at 12°C.

How much kilogram of each one is needed to make an 800 liter of water bath
at temperature of 35°C.

Answer 1

`m_(cold)=567kg\\\\m_(hot)=233kg`

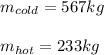
Step-by-step explanation:

Hello!

In this case, since equilibrium temperature problems involve the mass, specific heat and temperature change for the substances at different temperatures, we can write:

`m_(cold)C_(cold)(T_(eq)-T_(cold))=-m_(hot)C_(hot)(T_(eq)-T_(hot))`

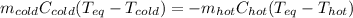
Thus, since we are talking about water and they both have the same specific heat, we can write:

`m_(cold)(T_(eq)-T_(cold))=-m_(hot)(T_(eq)-T_(hot))`

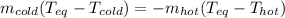
Now, we plug in the temperatures to obtain:

`m_(cold)(35-12)+m_(hot)(35-91)=0\\\\23m_(cold)-56m_(hot)=0`

Next, since the total volume of water is 800 L, since it has a density of 1kg/L, we infer the total mass is 800 kg; that is why we can write a 2x2 system of simultaneous equations:

`\left \{ {{23m_(cold)-56m_(hot)=0} \atop {m_(cold)+m_(hot)=800}} \right.`

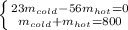
Thus, the masses of both cold and hot water turn out:

`m_(cold)=567kg\\\\m_(hot)=233kg`

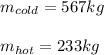
Best regards!