Question

Piedmont Hospital decides to go into the glove manufacturing business for themselves, considering their annual demand for surgical gloves is 25,000 pairs. It costs $25 to set up their production equipment and personnel, and 500 pairs can be produced each day. With their limited storage space it is estimated that it costs $0.05 to hold one pair of gloves in inventory for a year. Assuming 250 working days per year, perform a Production Order Quantity analysis. Set up the inventory problem and answer the following.a) What should their ORDER SIZE be if they wish to minimize total cost?b) For how many consecutive days will they produce surgical gloves for a given cycle?c) Comparing the results of the POQ here to the EOQ in the prior problem, which is the less expensive option for the hospital?(A) Ordering gloves (B) Producing gloves (C) They are equal in cost

Answer 1

The best order size to minimize cost will be 5,000

They will produce for 10 days in a row.

Step-by-step explanation:

D = annual demand 25,000

S= setup cost = ordering cost 25

H= Holding Cost = 0.05

`Q_(opt) = \sqrt{(2DS)/(H)}`

`Q_(opt) = \sqrt{(2(25,000)(25))/(0.05)}`

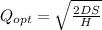
EOQ = 5,000

EDIT: there is insufficient information to solve the third question as the previous scenario wasn't attached.