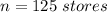Question

Wal-Mart conducted a study to check the accuracy of checkout scanners at its stores. At each of the 60 randomly selected Wal-Mart stores, 100 random items were scanned. The researchers found that 52 of the 60 stores had more than 2 items that were priced inaccurately (the national standards allow a maximum of 2 items out of 100 items priced accurately by the scanners). a) Construct a 95% confidence interval for proportion of Wal-Mart stores that have more than 2 items priced inaccurately per 100 items scanned and give a practical interpretation of this interval. (3 Points) b) Wal-Mart claims that 99% of its stores comply with the national standard on accuracy of price scanners. Comment on the believability of Wal-Mart’s claim based on your results in part (a). (1 Point) c) Determine the number of Wal-Mart stores that must be sampled in order to estimate the true proportion to within 0.05 with 90% confidence. (3 Points)

Answer 1

a

The 95% confidence interval is

`0.7811 <  p <  0.9529`

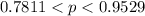
Generally the interval above can interpreted as

There is 95% confidence that the true proportion of Wal-Mart stores that have more than 2 items priced inaccurately per 100 items scanned lie within the interval

b

Generally 99% is outside the interval obtained in a above then the claim of Wal-mart is not believable

c

`n =  125  \  stores`

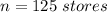
Explanation:

From the question we are told that

The sample size is n = 60

The number of stores that had more than 2 items price incorrectly is k = 52

Generally the sample proportion is mathematically represented as

`\^ p = ( k )/( n )`

=>
`\^ p = ( 52 )/( 60 )`

=>
`\^ p = 0.867`

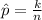
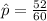
From the question we are told the confidence level is 95% , hence the level of significance is

`\alpha = (100 - 95 ) \%`

=>
`\alpha = 0.05`

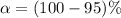
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  1.96`

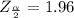
Generally the margin of error is mathematically represented as

`E =  Z_{(\alpha )/(2) } * \sqrt{(\^ p (1- \^ p))/(n) }`

=>
`E =  1.96  * \sqrt{( 0.867  (1- 0.867))/(60) }`

=>
`E =  0.0859`

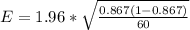
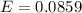
Generally 95% confidence interval is mathematically represented as

`\^ p -E <  p <  \^ p +E`

=>
`0.867  - 0.0859  <  p <  0.867  +  0.0859`

=>
`0.7811 <  p <  0.9529`

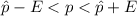
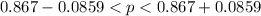
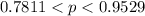
Generally the interval above can interpreted as

There is 95% confidence that the true proportion of Wal-Mart stores that have more than 2 items priced inaccurately per 100 items scanned lie within the interval

Considering question b

Generally 99% is outside the interval obtained in a above then the claim of Wal-mart is not believable

Considering question c

From the question we are told that

The margin of error is E = 0.05

From the question we are told the confidence level is 95% , hence the level of significance is

`\alpha = (100 - 95 ) \%`

=>
`\alpha = 0.05`

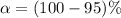
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  1.645`

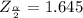
Generally the sample size is mathematically represented as

`n = [\frac{Z_{(\alpha )/(2) }}{E} ]^2 * \^ p (1 - \^ p )`

=>
`n=  [\frac{1.645 }}{0.05} ]^2 * 0.867  (1 - 0.867 )`

=>
`n =  125  \  stores`