Question

Each of five, standard, six-sided dice is rolled once. What is the probability that there is at least one pair but not a three-of-a-kind (that is, there are two dice showing the same value, but no three dice show the same value)

Answer 1

The probability that there is at least one pair but not a three of a kind is 0.6944.

Explanation:

We have the case when we have five dices and we roll them and we need that there is at least one pair but not a three of a king which is Two dice showing the same value, but no three dice showing the value.

Total no of outcomes =
`6^5 = 7776`

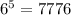
We will consider the other cases and then subtract them from the total outcomes.

No of outcomes of 5 of a kind = 6

No of outcomes 4 of a kind and 1 different = (6*5)*5 = 150

No of outcomes with 3 of a kind and 1 different pairs = (6*1*1*5*1)*5C2= 300

No of outcomes with 3 of a kind and two different = 6*5*4*10= 120*10=1200

No of outcomes when all are different = 6! = 720

These all the cases when subtracted from the total will represent the total cases in which there are two dice showing the same value.

Total cases = 6+150+300+1200+720

= 2376

Required no of outcomes = 7776-2376 = 5400

Probability =
`(5400)/(7776)` = 0.6944

Therefore the probability for the case of at least one pair but not a three of a kind is 0.6944.