Question

A group of researchers wants to know whether men are more likely than women to contract a novel coronavirus. They surveyed two random samples of 390 men and 360 women who were tested and found that 47 men and 52 women in the samples tested positive. Can you conclude that the proportion of positive tests among men is different from the proportion of positive tests among women? Use level of significance 10%. Procedure: Two means T (pooled) Hypothesis Test Step 1. Hypotheses Set-Up: H 0 : Select an answer = , where Select an answer the Select an answer and the units are Select an answer H a : Select an answer ? , and the test is Select an answer Step 2. The significance level α = % Step 3. Compute the value of the test statistic: Select an answer = (Round the answer to 3 decimal places) Step 4. Testing Procedure: (Round the answers to 3 decimal places) CVA PVA Provide the critical value(s) for the Rejection Region: Compute the P-value of the test statistic: left CV is and right CV is P-value is Step 5. Decision: CVA PVA Is the test statistic in the rejection region? Is the P-value less than the significance level? ? ? Conclusion: Select an answer Step 6. Interpretation: At 10% significance level we Select an answer have sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis.

Answer 1

Test statistic Z= 0.13008 < 1.96 at 0.10 level of significance

null hypothesis is accepted

There is no difference proportion of positive tests among men is different from the proportion of positive tests among women

Explanation:

Step(I):-

Given surveyed two random samples of 390 men and 360 women who were tested

first sample proportion

`p_(1) = (360)/(390) = 0.9230`

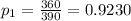
second sample proportion

`p_(2) = (47)/(52) = 0.9038`

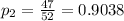
Step(ii):-

Null hypothesis : H₀ : There is no difference proportion of positive tests among men is different from the proportion of positive tests among women

Alternative Hypothesis:-

There is difference between proportion of positive tests among men is different from the proportion of positive tests among women

`Z = \frac{p_(1)- p_(2) }{\sqrt{PQ((1)/(n_(1) )+(1)/(n_(2) ) } }`

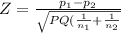
where

`P = (n_(1)p_(1) +n_(2) p_(2) )/(n_(1)+n_(2) )`

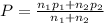
P = 0.920

`Z= \frac{0.9230-0.9038}{\sqrt{0.920 X0.08((1)/(390)+(1)/(52) } )}`

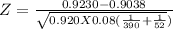
Test statistic Z = 0.13008

Level of significance = 0.10

The critical value Z₀.₁₀ = 1.645

Test statistic Z=0.13008 < 1.645 at 0.1 level of significance

Null hypothesis is accepted

There is no difference proportion of positive tests among men is different from the proportion of positive tests among women