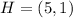Answer:
Explanation:
The attachment is not clear. However, the points of G and F are:
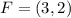
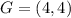
And the options are:
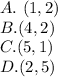
Required
Determine the coordinates of H
This question will be solved using distance formula, D
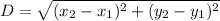
Since F is equidistant of G and H, the formula can be represented as:
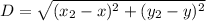 and
and
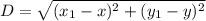
Where:

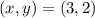
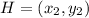
Substitute values for x , y , x2 and y2 in
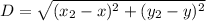
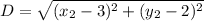
Square both sides:
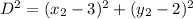
Substitute values for x , y , x1 and y1 in
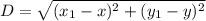

Square both sides:
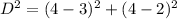
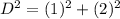
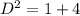
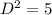
Substitute 5 for D^2 in
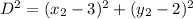
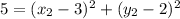
From the list of given options, the values of x and y that satisfy the above condition is: (5,1)
This is shown below
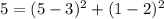
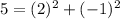
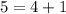
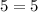
Other options do not satisfy this condition. Hence, the coordinates of H is: