Question

Suppose Upper F Superscript prime Baseline left-parenthesis x right-parenthesis equals 3 x Superscript 2 Baseline plus 7 and Upper F left-parenthesis 0 right-parenthesis equals 5. Find the value of Upper F left-parenthesis b right-parenthesis for b equals 0 comma 0.1 comma 0.2 comma 0.5 comma and 2.0.

Answer 1

It looks like you're given

F'(x) = 3x² + 7

and

F (0) = 5

and you're asked to find F(b) for the values of b in the list {0, 0.1, 0.2, 0.5, 2.0}.

The first is done for you, F (0) = 5.

For the remaining b, you can solve for F(x) exactly by using the fundamental theorem of calculus:

`F(x)=F(0)+\displaystyle\int_0^x F'(t)\,\mathrm dt`

`F(x)=5+\displaystyle\int_0^x(3t^2+7)\,\mathrm dt`

`F(x)=5+(t^3+7t)\bigg|_0^x`

`F(x)=5+x^3+7x`

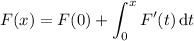
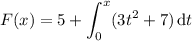
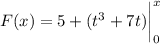
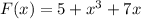
Then F (0.1) = 5.701, F (0.2) = 6.408, F (0.5) = 8.625, and F (2.0) = 27.

On the other hand, if you're expected to approximate F at the given b, you can use the linear approximation to F(x) around x = 0, which is

F(x) ≈ L(x) = F (0) + F' (0) (x - 0) = 5 + 7x

Then F (0) = 5, F (0.1) ≈ 5.7, F (0.2) ≈ 6.4, F (0.5) ≈ 8.5, and F (2.0) ≈ 19. Notice how the error gets larger the further away b gets from 0.

A better numerical method would be Euler's method. Given F'(x), we iteratively use the linear approximation at successive points to get closer approximations to the actual values of F(x).

Let y(x) = F(x). Starting with x₀ = 0 and y₀ = F(x₀) = 5, we have

x₁ = x₀ + 0.1 = 0.1

y₁ = y₀ + F'(x₀) (x₁ - x₀) = 5 + 7 (0.1 - 0) → F (0.1) ≈ 5.7

x₂ = x₁ + 0.1 = 0.2

y₂ = y₁ + F'(x₁) (x₂ - x₁) = 5.7 + 7.03 (0.2 - 0.1) → F (0.2) ≈ 6.403

x₃ = x₂ + 0.3 = 0.5

y₃ = y₂ + F'(x₂) (x₃ - x₂) = 6.403 + 7.12 (0.5 - 0.2) → F (0.5) ≈ 8.539

x₄ = x₃ + 1.5 = 2.0

y₄ = y₃ + F'(x₃) (x₄ - x₃) = 8.539 + 7.75 (2.0 - 0.5) → F (2.0) ≈ 20.164