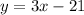Question

Line AB and line BC form a right angle at point B with points A (2,5) and B(8,3). what is the equation of line BC?​

Answer 1

y=3x-21

Explanation:

General outline

1. Find equation for line AB
2. Find equation for perpendicular line BC

Step 1. Find equation for line AB

Given points A(2,5) and B(8,3), line AB must contain them.

To calculate the slope,
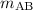`m_{\text{AB}}`, of line AB, use the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

`m_{\text{AB}}=((3)-(5))/((8)-(2))`

`m_{\text{AB}}=(-2)/(6)`

`m_{\text{AB}}=-(1)/(3)`

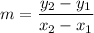
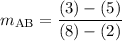
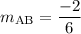
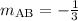
Since the slope isn't undefined, line AB must cross the y-axis somewhere. To find the y-intercept, build and equation in slope-intercept form:

`y=m_{\text{AB}}x+b_{\text{AB}}`

`y=\left(-(1)/(3) \right) x+b_{\text{AB}}`

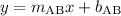
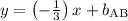
Substituting values for a known point (point A) on line AB...

`(5)=\left(-(1)/(3) \right) (2)+b_{\text{AB}}`

`5=-(2)/(3) +b_{\text{AB}}`

`(5)+(2)/(3) =(-(2)/(3) +b_{\text{AB}})+(2)/(3)`

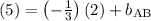
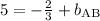
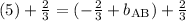
Finding a common denominator...

`(3)/(3)*5+(2)/(3) =b_{\text{AB}}`

`(15)/(3)+(2)/(3) =b_{\text{AB}}`

`(17)/(3)=b_{\text{AB}}`

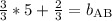
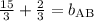
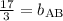
So, the equation for line AB is
`y=-(1)/(3) x +(17)/(3)`

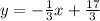
Step 2. Find equation for line BC

Since line AB and line BC form a right angle, they are perpendicular. Perpendicular lines have slopes that are opposite (opposite sign) reciprocals (fraction flipped upside-down) of each other. Stated another way, the slopes multiply to make negative 1.

`m_{\text{AB}}*m_{\text{BC}}=-1`

`\left( -(1)/(3) \right) *m_{\text{BC}}=-1`

`-3*\left( -(1)/(3) *m_{\text{BC}} \right) =-3*(-1)`

`m_{\text{BC}} =3`

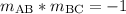
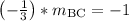
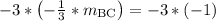
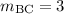
Since the slope isn't undefined, line BC must also cross the y-axis somewhere. To find the y-intercept, build and equation in slope-intercept form:

`y=m_{\text{BC}}x+b_{\text{BC}}`

`y=(3) x+b_{\text{BC}}`

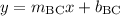
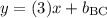
Substituting values for a known point (point B) on line BC...

`(3)=3 * (8)+b_{\text{BC}}`

`3=24+b_{\text{BC}}`

`(3)-24=(24+b_{\text{BC}})-24`

`-21=b_{\text{BC}}`

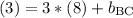
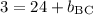
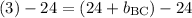
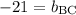
So, the equation for line BC is
`y=3 x -21`