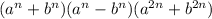Answer:
a.
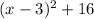
b.
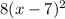
c.
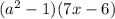 or
or
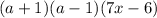
d.
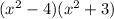 or
or
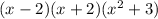
e.
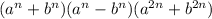
Explanation:
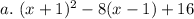
Expand
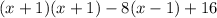
Open brackets
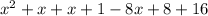
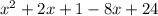
Collect Like Terms
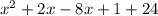
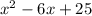
Express 25 as 9 + 16
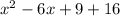
Factorize:
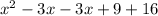
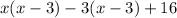
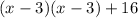
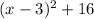
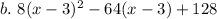
Expand

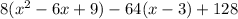
Open Brackets
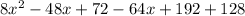
Collect Like Terms
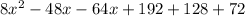
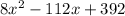
Factorize
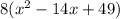
Expand the expression in bracket
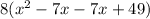
Factorize:
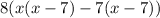
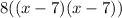
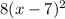
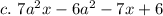
Factorize
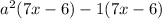
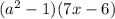
The answer can be in this form of further expanded as follows:
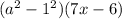
Apply difference of two squares
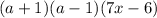
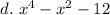
Express
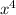 as
as
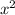
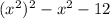
Expand
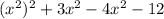
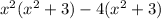
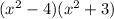
The answer can be in this form of further expanded as follows:
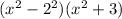
Apply difference of two squares
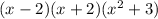
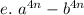
Represent as squares

Apply difference of two squares
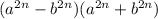
Represent as squares
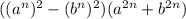
Apply difference of two squares