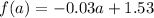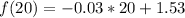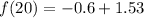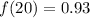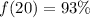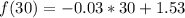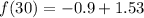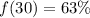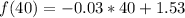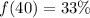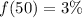Answer:
a.
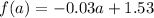
b. See Explanation
c. The slope is reasonable but the p intercept is not
d.
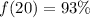
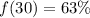
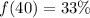
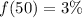
Explanation:
Given

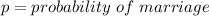
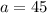 when
when
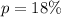
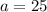 when
when
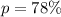
Solving (a): The linear function
We start by calculating the slope, m
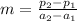
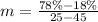
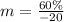
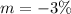

The function is then calculated as follows

This gives:

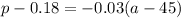
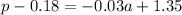
Solve for p

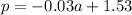
Hence,
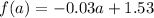
Solving (b): Interpret the slope and the p intercept
The slope is calculated as:

And it implies that, there is a 3% reduction in change of getting older as women get older
The p intercept implies that, there is a 1.53 chance for 0 years old female child to get married.
Solving (c): Is (b) reasonable
The slope is reasonable.
However, the p intercept is not because of the age of the woman
Solving (d): Determine f(20), f(30), f(40), f(50)
We have that: