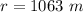Question

the maximum normal force a pilot can withstand is about eight times his weight. What is the maximum radius of curvature that a jet planes pilot, pulling out of a vertical dive

Answer 1

Complete Question

the maximum force a pilot can stand is about seven times his weight. what is the minimum radius of curvature that a jet plane's pilot, pulling out of a vertical dive, can tolerate at a speed of 250m/s?

Answer:

The value is
`r = (250^2 )/(6 * 9.8 )`

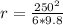
Step-by-step explanation:

From the question we are told that

The weight of the pilot is
`W = mg`

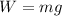
The maximum force a pilot can withstand is
`F_(max) = 7 W = 7 (mg)`

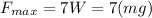
The speed is
`v = 250 \ m/s`

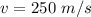
Generally the centripetal force acting on the pilot is equal to the net force acting on the pilot i.e

`F_c = F_(max) - mg`

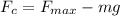
Here N is the normal force acting on the pilot

Now

`F_c = (m v^2 )/(r)`

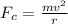
So

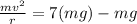
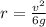
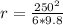
`(m v^2 )/(r) = 7(mg) - mg`

=>
`r = (v^2 )/(6g)`

=>
`r = (250^2 )/(6 * 9.8 )`

=>
`r = 1063 \ m`