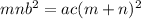Question

Сатре о

Find the condition that the roots of the quadratic equation
ax2 + cx + C =0
may be in the ratio m:n​

Answer 1

`mnb^2 = ac(m+n)^2`

Explanation:

Given

`ax^2 +bx + c = 0`

Required

Condition that the roots is in m : n

Let the roots of the equation be represented as: mA and nA

A quadratic equation has the form:

`x^2 + (sum\ of\ roots)x + (product\ of\ roots)=0`

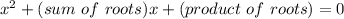
or

`x^2 - ((b)/(a))x + (c)/(a) = 0`

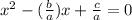
We have the roots to be mA and nA.

So, the sum is represented as:

`Sum = mA + nA`

`Sum = A(m + n)`

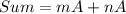
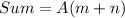
And the product is represented as:

`Product = mA * nA`

`Product = mnA^2`

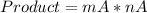
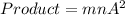
By comparing:

`x^2 + (sum\ of\ roots)x + (product\ of\ roots)=0`

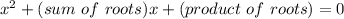
with

`x^2 - ((b)/(a))x + (c)/(a) = 0`

`Sum = -(b)/(a)`

`Product = (c)/(a)`

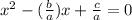
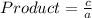
So, we have:

`Sum = -(b)/(a)`

`A(m + n) = -(b)/(a)`

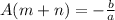
Make A the subject:

`A = (-b)/(a(m+n))`

`Product = (c)/(a)`

`mnA^2 = (c)/(a)`

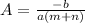
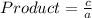
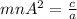
Substitute
`A = (-b)/(a(m+n))`

`mn((-b)/(a(m+n)))^2 = (c)/(a)`

`mn(b^2)/(a^2(m+n)^2) = (c)/(a)`

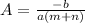
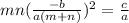
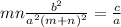
Multiply both sides by a

`a * mn(b^2)/(a^2(m+n)^2) = (c)/(a) * a`

`(mnb^2)/(a(m+n)^2) = c`

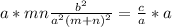
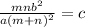
Cross Multiply:

`mnb^2 = ac(m+n)^2`

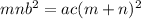
Hence, the condition that the ratio is in m:n is

`mnb^2 = ac(m+n)^2`