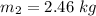Question

An insulated rigid tank with a volume of 0.57 m3, contains 4 kg of Argon gas at 450 kPa and 30 C. A valve is now opened, and the Argon is slowly allowed to escape until the pressure inside drops to 200 kPa. Assuming the Argon remaining inside the tank has undergone a reversible, adiabatic process, determine the final mass in the tank,

Answer 1

The value is
`m_2 = 2.46 \ kg`

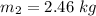
Step-by-step explanation:

From the question we are told that

The volume of the tank is
`V = 0.57 \ m^3`

The mass of the Argon it contains is
`m = 4 \ kg`

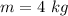
The initial pressure on of the gas is
`P_1 = 450 kPa = 450 *10^(3) \ Pa`

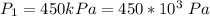
The initial temperature is
`T_1 = 30^oC = 30 + 273 = 303 \ K`

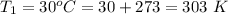
The new pressure inside the tank is
`P_2 = 200 \ kPa = 200 *10^(3) \ Pa`

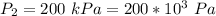
Gnerally given that the Argon remaining inside the tank has undergone a reversible, adiabatic process, then the final temperature of the Argon gas is mathematically represented as

`T_2 = T_1 * [(P_2)/(P_1) ]^{ ((k - 1 ))/(k) }`

Here k is the specific heat ratio of Argon with value
`k = 1.667`

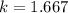
So

`T_2 = 303 * [(200)/(450) ]^{ ((1.667- 1 ))/(1.667) }`

=>
`T_2 = 219 \ K`

Generally from the ideal gas equation

`PV = mRT_2`

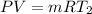
So

`(P_1V)/(P_2V) =( m_1 * R * T_1 )/( m_2 * R * T_2)`

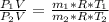
Here R is the gas constant with value
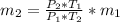
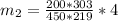
`R = 8.314 \J \ K^(-1)\ mol^(-1)`

=>
`m_2 = (P_2 * T_1 )/( P_1 * T_2 ) * m_1`

=>
`m_2 = (200 * 303 )/( 450 * 219 ) * 4`

=>
`m_2 = 2.46 \ kg`