Question

3×_5=16 and 3×=21

the first equation is a true statement for a certain value of x.

can you explain why the second equation must also be true for the same value of x?​

Answer 1

Understanding:

First, let's try simplifying the first equation as much as we can. As you know, you can add, subtract, multiply, divide, etc on both sides of the equation and it will remain the same value. To simplify
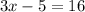`3x-5=16` we can simply add 5 to both sides to cancel the -5 on the left-hand side. That will give us
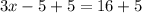`3x-5 +5=16+5`, notice we added the 5 to both sides. The +5 cancels -5 and 16+5 is 21, which evaluates to
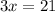`3x=21`. And this equation looks familiar, it's our second equation actually. That's why both equations are the same, and in that x value that makes the first equation true, it will also do the same for the second equation. If you want to actually find the value of x which makes the equation true, you can simply divide the 21 on the right-side by 3 to make x coefficient equal to 1,
`(3x)/(3) =(21)/(3)`, and that gives us,
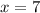`x=7`. When x is 7 both equations are true.

Answer 2

We conclude that the second equation must also be true for the same value of x because the value x = 7 satisfies the 2nd equation too.

Explanation:

Given the first equation

`3x-5=16`

Add 5 to both sides

`3x-5+5=16+5`

simplify

`3x=21`

Divide both sides by 3

`(3x)/(3)=(21)/(3)`

simplify

`x=7`

Thus, x = 7 is a value that satisfies the first equation.

Now, put x = 7 in the 2nd question to check whether x = 7 satisfies the equation or not.

3x = 21

3(7) = 21 ∵ x = 7

21 = 21

Thus, x = 7 also satisfies the 2nd equation.

Therefore, we conclude that the second equation must also be true for the same value of x because the value x = 7 satisfies the 2nd equation too.