Question

(20 points) A 1 mm diameter tube is connected to the bottom of a container filled with water to a height of 2 cm from the bottom. Air flows from the tube into the liquid and creates spherical bubbles with diameter about the diameter of the tube (1 mm). Everything is at 298 K. The tube is short but is connected to a much longer 2 m long hose that is 6 mm in diameter. The hose is connected to the gas supply. If there is no gas flow the water will leak into the tube and into the supply hose. When gas flows the water is blocked from entering the tube and bubbling starts. State all assumptions in answering the following questions. (a) What should be the minimum air flow rate and the gas supply pressure to keep the water from leaking back into the tube? (b) Is the flow in the hose laminar or turbulent? Is the flow in the tube laminar or turbulent?

Answer 1

Given :

h = 2 cm

Diameter of the tube , d = 1 mm

Diameter of the hose, D = 6 mm

Between 1 and 2, by applying Bernoulli's principle, we get

As point 1 is just below the free surface of liquid, so

`$P_1=P_(atm) \text{ and} \ V_1=0$`

`$(P_(atm))/(\rho g)+(v_1^2)/(2g) +h = (P_2)/(\rho g)$`

`$(101.325)/(1000 * 9.81)+0.02 =(P_2)/(\rho g)$`

`$P_2 = 111.35 \ kPa$`

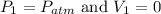
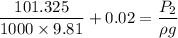
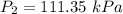
Therefore, 111.325 kPa is the gas supply pressure required to keep the water from leaking back into the tube.

Velocity at point 2,

`$V_2=\sqrt{\left((111.135)/(\rho g)+0.02}\right)* 2g$`

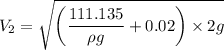
= 1.617 m/s

Flow of water,
`$Q_2 = A_(tube) * V_2$`

`$=(\pi)/(4) * (10^(-3))^2 * 1.617 $`

`$1.2695 * 10^(-6) \ m^3/s$`

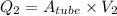
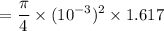
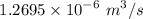
Minimum air flow rate,

`$Q_2 = Q_3 = A_(hose) * V_3$`

`$V_3 = (Q_2)/((\pi)/(4)D^2)$`

`$V_3 = (1.2695 *10^(-6))/(\pi* 0.25 * 36 * 10^(-6))$`

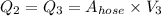
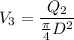
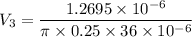
= 0.0449 m/s

b). Reynolds number in hose,

`$Re = (\rho V_3 D)/(\mu) = (V_3 D)/(\\u)$`

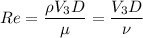
υ for water at 25 degree Celsius is
`$8.9 * 10^(-7) \ m^2/s$`

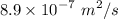
υ for air at 25 degree Celsius is
`$1.562 * 10^(-5) \ m^2/s$`

`$Re_(hose)=(0.0449 * 6 * 10^(-3))/(1.562 * 10^(-5))$`

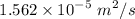
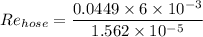
= 17.25

Therefore the flow is laminar.

Reynolds number in the pipe

`$Re = (V_2 d)/(\\u) = (1.617 * 10^(-3))/(8.9 * 10^(-7))$`

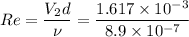
= 1816.85, which is less than 2000.

So the flow is laminar inside the tube.