Answer:
The 95% confidence interval estimate of the proportion of people who say that they voted
(0.67122 , 0.72798)
Explanation:
Step(i):-
In a recent survey of 1002 people, 701 said that they voted in a recent presidential election.
Sample proportion
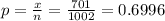
Step(ii)
The 95% confidence interval estimate of the proportion of people who say that they voted
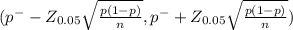
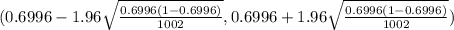
(0.6996 - 1.96 X 0.01448 , 0.6996 + 1.96 X 0.01448)
(0.6996 - 0.02838 , 0.6996 + 0.02838)
(0.67122 , 0.72798)
Final answer:-
The 95% confidence interval estimate of the proportion of people who say that they voted
(0.67122 , 0.72798)