Answer:
Approximately
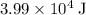 (assuming that the melting point of ice is
(assuming that the melting point of ice is
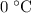 .)
.)
Step-by-step explanation:
Convert the unit of mass to kilograms, so as to match the unit of the specific heat capacity of ice and of water.
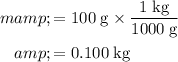
The energy required comes in three parts:
- Energy required to raise the temperature of that
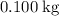 of ice from
of ice from
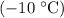 to
to
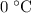 (the melting point of ice.)
(the melting point of ice.) - Energy required to turn
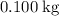 of ice into water while temperature stayed constant.
of ice into water while temperature stayed constant. - Energy required to raise the temperature of that newly-formed
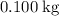 of water from
of water from
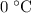 to
to
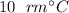 .
.
The following equation gives the amount of energy
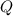 required to raise the temperature of a sample of mass
required to raise the temperature of a sample of mass
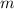 and specific heat capacity
and specific heat capacity
 by
by
 :
:
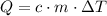 ,
,
where
 is the specific heat capacity of the material,
is the specific heat capacity of the material,
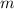 is the mass of the sample, and
is the mass of the sample, and
 is the change in the temperature of this sample.
is the change in the temperature of this sample.
For the first part of energy input,
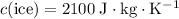 whereas
whereas
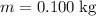 . Calculate the change in the temperature:
. Calculate the change in the temperature:
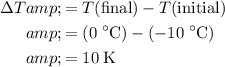 .
.
Calculate the energy required to achieve that temperature change:
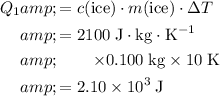 .
.
Similarly, for the third part of energy input,
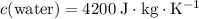 whereas
whereas
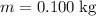 . Calculate the change in the temperature:
. Calculate the change in the temperature:
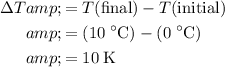 .
.
Calculate the energy required to achieve that temperature change:
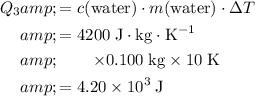 .
.
The second part of energy input requires a different equation. The energy
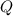 required to melt a sample of mass
required to melt a sample of mass
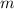 and latent heat of fusion
and latent heat of fusion
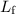 is:
is:
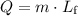 .
.
Apply this equation to find the size of the second part of energy input:
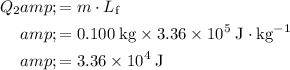 .
.
Find the sum of these three parts of energy:
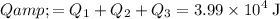 .
.