A geometric sequence is shown below. −12,−2,−8,−32,... What is an explicit representation for the nth term of the sequence? A.f(n)=12(−4)n B. f(n)=−12(4)n−1 C. f(n)=−12(4)n D. f…

Question

asked Jan 23, 2021 137k views

1 Answer

Siddharth Kamaria · Answer 1 · 2021-01-27T02:33:02+0000

Answer:

An explicit representation for the nth term of the sequence:

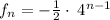
$f_n=-(1)/(2)\cdot \:4^(n-1)$

It means, option (B) should be true.

Explanation:

Given the geometric sequence

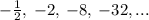
$-(1)/(2),\:-2,\:-8,\:-32,...$

A geometric sequence has a constant ratio, denoted by 'r', and is defined by

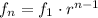
$f_n=f_1\cdot r^(n-1)$

Determining the common ratios of all the adjacent terms

$(-2)/(-(1)/(2))=4,\:\quad (-8)/(-2)=4,\:\quad (-32)/(-8)=4$

As the ratio is the same, so

r = 4

Given that f₁ = -1/2

substituting r = 4, and f₁ = -1/2 in the nth term

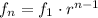
$f_n=f_1\cdot r^(n-1)$

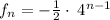
$f_n=-(1)/(2)\cdot \:4^(n-1)$

Thus, an explicit representation for the nth term of the sequence:

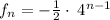
$f_n=-(1)/(2)\cdot \:4^(n-1)$

It means, option (B) should be true.