Question

Find the particular solution to y ' = 2sin(x) given the general solution is y = C - 2cos(x) and the initial condition y of pi over 3 equals 1 . (5 points)

-2cos(x)
closeIncorrect
3 - 2cos(x)
checkCorrect
2 - 2cos(x)
-1 - 2cos(x)

Answer 1

`y=2-2\cos(x)`

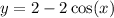
Explanation:

We have the differential:

`y^\prime=2\sin(x)`

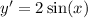
With the general solution:

`y=C-2\cos(x)`

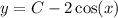
And we want to find the particular solution such that it satisfies the initial condition:

`\displaystyle y\Big((\pi)/(3)\Big)=1`

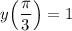
So, we have:

`y=C-2\cos(x)`

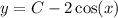
Substituting π/3 for x and 1 for y yields:

`\displaystyle 1=C-2\cos\Big( (\pi)/(3) \Big)`

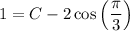
Solve for C. Evaluate:

`\displaystyle 1=C-2((1)/(2))`

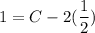
Simplify:

`1=C-1`

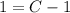
Hence:

`C=2`

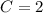
Therefore, our particular solution will be:

`y=2-2\cos(x)`

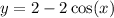
Hence, our answer is C