Answer:
11
Explanation:
Because 4 and 6 aren't co prime we can't start the chinese remainder theorem
so first we check
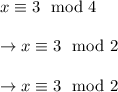
because 4 = 2*2
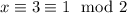
and the other one

so now we have
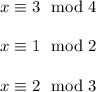
but the mod 2 we don't need it
so now we have
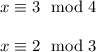
for the first one we can say that
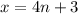
so we plug in that in the second one
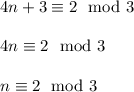
we can say that
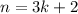
so for x
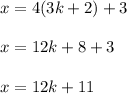
so if k=0
a solution is 11
we check if it works
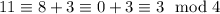
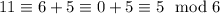
so it works so the smallest solution is 11