Question

Tomika heard that the diagonals of a rhombus are perpendicular to each other. Help her test her conjecture. Graph quadrilateral ABCD on a coordinate grid with A(1, 4), B(6, 6), C(4, 1), and D(–1, –1).

a. A rhombus has 4 sides that are equal length. Is ABCD a rhombus? Show how you know.


b. Write the equations of the lines on which the diagonals lie. That is, write the equations of lines AC and BD.


c. Compare the slopes of lines AC and BD. What do you notice?

Answer 1

a. The four sides of the quadrilateral ABCD are equal, therefore, ABCD is a rhombus

b. The equation of the diagonal line AC is y = 5 - x

The equation of the diagonal line BD is y = 5 - x

c. The diagonal lines AC and BD of the quadrilateral ABCD are perpendicular to each other

Explanation:

The vertices of the given quadrilateral are;

A(1, 4), B(6, 6), C(4, 1) and D(-1, -1)

a. The length, l, of the sides of the given quadrilateral are given as follows;

`l = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

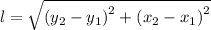
The length of side AB, with A = (1, 4) and B = (6, 6) gives;

`l_(AB) = \sqrt{\left (6-4 \right )^(2)+\left (6-1 \right )^(2)} = √(29)`

The length of side BC, with B = (6, 6) and C = (4, 1) gives;

`l_(BC) = \sqrt{\left (1-6 \right )^(2)+\left (4-6 \right )^(2)} = √(29)`

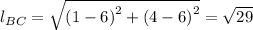
The length of side CD, with C = (4, 1) and D = (-1, -1) gives;

`l_(CD) = \sqrt{\left (-1-1 \right )^(2)+\left (-1-4 \right )^(2)} = √(29)`

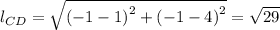
The length of side DA, with D = (-1, -1) and A = (1,4) gives;

`l_(DA) = \sqrt{\left (4-(-1) \right )^(2)+\left (1-(-1) \right )^(2)} = √(29)`

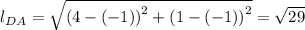
Therefore, each of the lengths of the sides of the quadrilateral ABCD are equal to √(29), and the quadrilateral ABCD is a rhombus

b. The diagonals are AC and BD

The slope, m, of AC is given by the formula for the slope of a straight line as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

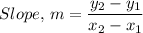
Therefore;

`Slope, \, m_(AC) =(1-4)/(4-1) = -1`

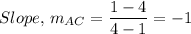
The equation of the diagonal AC in point and slope form is given as follows;

y - 4 = -1×(x - 1)

y = -x + 1 + 4

The equation of the diagonal AC is y = 5 - x

`Slope, \, m_(BD) =(-1-6)/(-1-6) = 1`

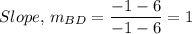
The equation of the diagonal BD in point and slope form is given as follows;

y - 6 = 1×(x - 6)

y = x - 6 + 6 = x

The equation of the diagonal BD is y = x

c. Comparing the lines AC and BD with equations, y = 5 - x and y = x, which are straight line equations of the form y = m·x + c, where m = the slope and c = the x intercept, we have;

The slope m for the diagonal AC = -1 and the slope m for the diagonal BD = 1, therefore, the slopes are opposite signs

The point of intersection of the two diagonals is given as follows;

5 - x = x

∴ x = 5/2 = 2.5

y = x = 2.5

The lines intersect at (2.5, 2.5), given that the slopes, m₁ = -1 and m₂ = 1 of the diagonals lines satisfy the condition for perpendicular lines m₁ = -1/m₂, therefore, the diagonals are perpendicular.