Answer:
Vertex form:
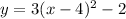
Vertex: (4, -2)
Explanation:
Hello!
We have to complete the square, and then simplify.
Solve:
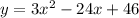

Take the coefficient of the second term, divide it by 2, and square it.
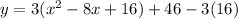
Balance your equation by subtracting what you added. Simplify.
The equation in vertex form is
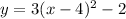
The vertex is (4,-2)
Vertex form
Vertex form is f(x) = a(x - h)² + k, where (h, k) is the vertex.