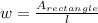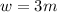Answer:
The width of the rectangle given is equal to 3m.
Explanation:
In order to solve this question we need to know that the areas of the rectangle is equal to
 , where "l" is length and "w" is width. So know in order to solve this question we would have to find out the unknown width by using area and the length of the triangle. Based on the formula I wrote down earlier we can understand the following.....
, where "l" is length and "w" is width. So know in order to solve this question we would have to find out the unknown width by using area and the length of the triangle. Based on the formula I wrote down earlier we can understand the following.....

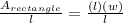
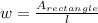
Just now we found out the formula that we can use to solve for the width when we know the area and the length of the rectangle. Now in order to get the answer we just have to plug in the values we know, and we get........