Answer:
For the value of hypotenuse can be irrational, sum of squares of other two legs might be imperfect square number.
Explanation:
We all know, the Pythagorean theorem can be stated as follows:
The sum of squares of two legs of a right angled triangle is equal to the square of the hypotenuse.
i.e.

Where,
 is the hypotenuse and
is the hypotenuse and
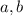 are the two other legs of the right angled triangle.
are the two other legs of the right angled triangle.
Given that:
 and
and
 are rational numbers.
are rational numbers.
To find:
Situation for which
 is irrational.
is irrational.
Square of a rational number is always rational.
So,
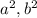 both will be rational.
both will be rational.
And sum of squares of two rational numbers will also be rational.
Therefore,
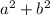 will also be rational.
will also be rational.
and
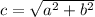
For the value of
 can be irrational, sum of squares of other two legs might be imperfect square number.
can be irrational, sum of squares of other two legs might be imperfect square number.