Question

Can someone explain this problem to me?? After a price reduction of x%, an item has its price increased to its original value. What was the percent of increase? Express your answer as a common fraction in terms of x.

Answer 1

`(-100(100+x))/((x-100))`

Explanation:

Let the original price of the item = p

Let there was q% of increase on the original value, so

the printed price of the item,
`C= p+p (q)/(100)=p(1+(q)/(100))`

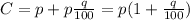
After a price reduction of x%, the has its price increased to its original value, so,

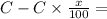`C-C* \frac {x}{100} =` original price + increased price

`p(1+(q)/(100))-p(1+(q)/(100))* \frac {x}{100} = p+p`

`(1+(q)/(100))-(1+(q)/(100))* (x)/(100) =2`

`-(1+(q)/(100))* (x)/(100) =2-1-(q)/(100)`

`-(1+(q)/(100))* (x)/(100) =1-(q)/(100)`

`(1+(q)/(100))* (x)/(100) =(q)/(100)-1`

`(x)/(100)+(q)/(100)*(x)/(100)-(q)/(100)=-1`

`x+x * (q)/(100)-q=-100`

`q((x)/(100)-1)=-100-x`

`q=(-100(100+x))/((x-100))`

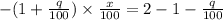
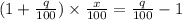
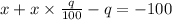
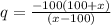
Hence, the percent of the increase is
`(-100(100+x))/((x-100))`