Question

The standard deviation is approximately??​

Answer 1

`SD = \$ 239`

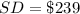
Explanation:

Given

`\$277.36, \$269.29, \$307.98, \$361.63, \$407.97,\\ \$442.99, \$601.71, \$693.64, \$870.21, \$970.60`

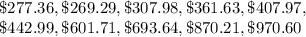
Required

Determine the standard deviation

First, we calculate the mean.

`Mean = (\$277.36+ \$269.29+ \$307.98+ \$361.63+ \$407.97+ \$442.99+ \$601.71+ \$693.64+ \$870.21+ \$970.60)/(10)`

`Mean = (\$5203.38)/(10)`

`Mean = \$520.338`

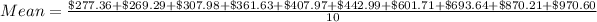
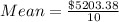
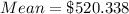
`Mean = \$520.34` --- approximately

Next, subtract the mean from each data

`\$277.36 - \$520.34 =-\$242.98`

`\$269.29 - \$520.34 = -\$251.05`

`\$307.98 - \$520.34 = -\$212.36`

`\$361.63 - \$520.34 = -\$158.71`

`\$407.97 - \$520.34 = -\$112.37`

`\$442.99 - \$520.34 = -\$77.35`

`\$601.71 - \$520.34 = \$81.37`

`\$693.64 - \$520.34 = \$173.3`

`\$870.21 - \$520.34 =\$349.87`

`\$970.60 - \$520.34 =\$450.26`

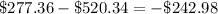
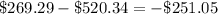
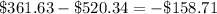
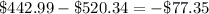
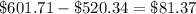
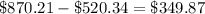
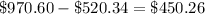
Square the results above

`(-\$242.98)^2 = \$59039.2804`

`(-\$251.05)^2 =\$63026.1025`

`(-\$212.36)^2 =\$45096.7696`

`(-\$158.71)^2 =\$25188.8641`

`(-\$112.37)^2 =\$12627.0169`

`(-\$77.35)^2 =\$5983.0225`

`(-\$81.37)^2 =\$6621.0769`

`(-\$173.3)^2 =\$30032.89`

`(-\$349.87)^2 =\$122409.0169`

`(-\$450.26)^2 =\$202734.0676`

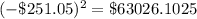
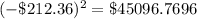
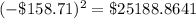
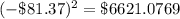
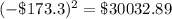
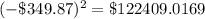
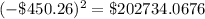
Add the squared results

`\$59039.2804 + \$63026.1025 + \$45096.7696 + \$25188.8641 + \$12627.0169 + \$5983.0225 +\$6621.0769 + \$30032.89 + \$122409.0169 + \$202734.0676`

`= \$572758.1074`

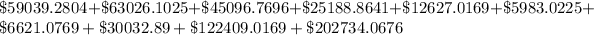
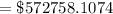
Divide by number of data, to get the variance

`Variance = (\$572758.1074)/(10)`

`Variance = \$57275.81074`

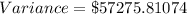
Square the above, to get the standard deviation

`SD = √(\$57275.81074)`

`SD = \$ 239.323652697`

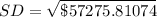
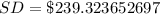
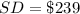`SD = \$ 239` --- approximated