Question

Type the correct answer in the box. Round your answer to the nearest integer.

In the figure, if m∠ABD = 120º, then m∠ADC =
º.

Answer 1

m∠ADC = 132

Explanation:

Answer 2

m∠ADC = 132°

Explanation:

Use sine rule to find m<ADB

`(b)/(sin(B)) = (d)/(sin(D))`

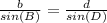
b = AD = 35

B = m∠ABD = 120º

d = AB = 30

D = m∠ADB = ?

Plug in the values

`(35)/(sin(120)) = (30)/(sin(D))`

`(35)/(sin(120)) = (30)/(sin(D))`

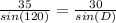
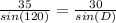
Cross multiply

`35 * sin(D) = 30 * sin(120)`

Divide both sides by 35

`(35 * sin(D))/(35) = (30 * sin(120))/(35)`

`sin(D) = (30 * sin(120))/(35)`

`sin(D) = 0.7423`

`D = sin^(-1)(0.7423)`

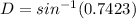
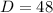`D = 48` (nearest integer)

D = m∠ADB = 48°

m∠ADC = 180 - m∠ADB (angles on a straight line)

m∠ADC = 180 - 48° (substitution)

m∠ADC = 132°