Question

A gas occupies 200ml at a temperature of 26 degrees Celsius and 76mmHg pressure. Find the volume at -3degree Celsius with the pressure remaining constant.

Answer 1

184.62 ml

Step-by-step explanation:

Let
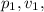`p_1, v_1,` and
`T_1` be the initial and
`p_2, v_2,` and
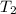`T_2` be the final pressure, volume, and temperature of the gas respectively.

Given that the pressure remains constant, so

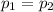`p_1=p_2` ...(i)

`v_1` = 200 ml

`T_1= 26 ^(\circ)C = 273+26 =299` K

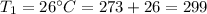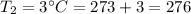`T_2= 3 ^(\circ)C = 273+3 =276` K

From the ideal gas equation, pv=mRT

Where p is the pressure, v is the volume, T is the temperature in Kelvin, m is the mass of air in kg, R is the specific gas constant.

For the initial condition,

`p_1v_1=mRT_1 \\\\mR= (p_1v_1)/(T_1)\cdots(ii)`

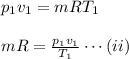
For the final condition,

`p_2v_2=mRT_2 \\\\mR= (p_2v_2)/(T_2)\cdots(iii)`

Equating equation (i), and (ii)

`(p_1v_1)/(T_1)=(p_2v_2)/(T_2)`

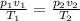
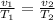`(v_1)/(T_1)=(v_2)/(T_2)` [from equation (i)]

`v_2=(T_2)/(T_1) * v_1`

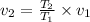
Putting all the given values, we have

`v_2=(276)/(299) * 200 = 184.62 \; ml`

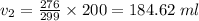
Hence, the volume of the gas at 3 degrees Celsius is 184.62 ml.