Question

I guess I'm lacking in differential equations. I couldn't solve this question. Can you help me?

Answer 1

See below.

Explanation:

We are given
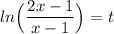`\displaystyle ln \Big ( (2x-1)/(x-1) \Big ) = t` and we want to find the first derivative of this function.

We can use the derivative of any function inside a natural log, denoted by
`\displaystyle (d)/(dx) \text{ln} \ u = ((d)/(dx) u)/(u)`, where u represents any function.

Let's take the derivative of the whole function with respect to x. This will look like:

• 
  `\displaystyle (d)/(dx) \displaystyle \Big [ ln \Big ( (2x-1)/(x-1) \Big ) = t \Big ] = ((d)/(dx) ((2x-1)/(x-1)) )/((2x-1)/(x-1) ) = (dt)/(dx)`

Let's take the derivative of the inside function,
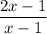`\displaystyle (2x-1)/(x-1)`, first. We will need the quotient rule, which is:

• 
  `\displaystyle (d)/(dx) \Big [ (f(x))/(g(x)) \Big] = (g(x) \cdot (d)/(dx)f(x)-f(x)\cdot (d)/(dx)g(x) )/([g(x)]^2)`

Here we have f(x) = 2x - 1 and g(x) = x - 1. Let's plug these values into the formula above:

• 
  `\displaystyle (d)/(dx) \Big [ (2x-1)/(x-1) \Big ] = ([(x-1)\cdot 2 ] - [(2x-1) \cdot 1])/((x-1)^2)`
• 
  `\displaystyle (d)/(dx) \Big [ (2x-1)/(x-1) \Big ] = (2x-2-2x+1)/((x-1)^2)`
• 
  `\displaystyle (d)/(dx) \Big [ (2x-1)/(x-1) \Big ] = (-1)/((x-1)^2)`

Now, we can substitute this back into the original equation for the derivative of the entire function.

• 
  `\displaystyle (dt)/(dx) = ((-1)/((x-1)^2) )/((2x-1)/(x-1) )`

Multiply the numerator by the reciprocal of the denominator.

• 
  `\displaystyle (dt)/(dx) = (-1)/((x-1)^2) \cdot (x-1)/(2x-1)`

The (x - 1)'s cancel out and we are left with:

• 
  `\displaystyle (dt)/(dx) = (-1)/((x-1)) \cdot (1)/(2x-1)`

This can be further simplified to a single fraction:

• 
  `\displaystyle (dt)/(dx) =(-1)/((x-1)(2x-1))`

Now we have dt/dx, but we want to find dx/dt. Therefore, we can flip the equation and have it in terms of dx/dt:

• 
  `\displaystyle (dx)/(dt) =((x-1)(2x-1))/(-1)`
• 
  `\displaystyle (dx)/(dt) =-(x-1)(2x-1)`

This can be further simplified to fit the expression the problem gives for dx/dt:

• 
  `\displaystyle (dx)/(dt) =(x-1)(1-2x)`

This is equivalent to the equation in the problem; therefore, the verification is complete.

Answer 2

See Explanation.

General Formulas and Concepts:

Pre-Algebra

• Equality Properties

• Reciprocals

Algebra II

• Log/Ln Property:
  `ln((a)/(b) ) = ln(a) - ln(b)`

Calculus

Derivatives

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Chain Rule:
`(d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Derivative of Ln:
`(d)/(dx) [ln(u)] = (u')/(u)`

Explanation:

Step 1: Define

`ln((2x-1)/(x-1) )=t`

Step 2: Differentiate

1. Rewrite:
   `t = ln((2x-1)/(x-1))`
2. Rewrite [Ln Properties]:
   `t = ln(2x-1) - ln(x - 1)`
3. Differentiate [Ln/Chain Rule/Basic Power Rule]:
   `(dt)/(dx) = (1)/(2x-1) \cdot 2 - (1)/(x-1) \cdot 1`
4. Simplify:
   `(dt)/(dx) = (2)/(2x-1) - (1)/(x-1)`
5. Rewrite:
   `(dt)/(dx) = (2(x-1))/((2x-1)(x-1)) - (2x-1)/((2x-1)(x-1))`
6. Combine:
   `(dt)/(dx) = (-1)/((2x-1)(x-1))`
7. Reciprocate:
   `(dx)/(dt) = -(2x-1)(x-1)`
8. Distribute:
   `(dx)/(dt) = (1-2x)(x-1)`