Question

An insurance company is thinking about offering discounts on its life insurance policies to nonsmokers. As part of its analysis, it selects 200 men who are 50 years old and asks them if they smoke at least one pack of cigarettes per day, and if they have ever suffered from heart disease. The results indicate that 20 out of 80 smokers and 15 out of 120 nonsmokers suffer from heart disease. At 5% level of significance the conclusion is:

Answer 1

Test statistic

|Z| = 2.996 > 1.96 at 5% level of significance

Null hypothesis is accepted

There is difference between smokers and non-smokers

Step-by-step explanation:

Step(i):-

Given size of the sample = 200

First Sample proportion

`p^(-) _(1) = (20)/(80) = 0.25`

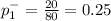
Second sample proportion

`p^(-) _(2) = (15)/(120) = 0.125`

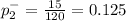
Null Hypothesis : p₁ = p₂

Alternative Hypothesis : p₁≠p₂

Step(ii):-

Test statistic

`Z = \frac{p^(-) _(1)-p^(-) _(2) }{\sqrt{PQ((1)/(n_(1) ) +(1)/(n_(2) ) )} }`

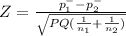
Where

`P = (n_(1) p_(1) + n_(2) p_(2) )/(n_(1)+n_(2) )`

`P = (200X 0.25+ 200 X 0.125 )/(400 ) = 0.185`

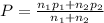
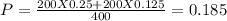
Q = 1-P = 0.8125

`Z = \frac{0.25-0.125 }{\sqrt{0.185X0.8125((1)/(200) +(1)/(200 ) )} }`

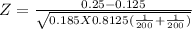
Z = -2.996

The calculated value |Z| = 2.996 > 1.96 at 5% level of significance

Null hypothesis is accepted

There is difference between smokers and non-smokers