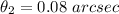Answer:
The value is
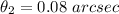
Step-by-step explanation:
From the question we are told that
The first wavelength is

The first angular size is
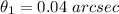
The second wavelength is
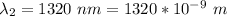
Generally according to Rayleigh Criterion we have that

given every other thing remains constant we have that
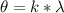
Here k represented constant so
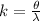
=>

=>
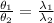
So
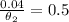
=>