Question

Suppose that 2% of produced computers by a company have defects, and defects occur independently of each other. a) Find the probability of exactly 2 defective computers in a shipment of 100 computers. b) The probability that a computer support specialist needs to test at least N computers in order to find one defective computer is 0.6676. Find N.

Answer 1

a) P(exactly two defectives) = 0.2734

b) N
`\simeq` 55

Explanation:

From the given information:

P(exactly two defectives) = P(X =2) =
`^(100)C_2 * ( 0.02)^2 *(1-0.02)^(100-2)`

`= (100!)/(2!(100-2)!) * ( 0.02)^2 *(0.98)^(98)`

`= 4950 * 4 * 10^(-4) * 0.1380878341`

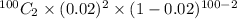
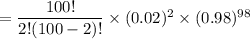
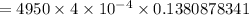
= 0.2734

Thus, P(exactly two defectives) = 0.2734

b)

To find:

P(X ≥ 1 )

let X be the random variable that obeys a binomial distribution, X represents the number of defectives,

∴

`X \sim B ( N, 0.02)`

`P(X \ge 1 ) = 1 - P(X < 1) \\ \\ P(X \ge 1 ) = 1 - P(X = 0)`

`0.6676 = 1 - ^NC_0 * (0.02)^0 (0.98)^N`

`0.6676 = 1 - (0.98)^N`

`(0.98)^N = 1 - 0.6676`

`(0.98)^N = 0.3324`

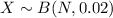
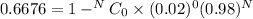
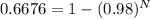
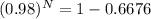
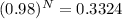
N log (0.98) = log (0.3324)

`N = (log \ 0.3324)/(log \ 0.98)`

N = 54.51824841

N
`\simeq` 55