Question

A solid sphere made of plastic density of 1350 kg/m3 has a radius of 35.0 cm. It is suspended by a massless cord. 75% of its volume is in water and 25% of it is in oil. The density of water is 1000 kg/m3 and the density of the oil is 850 kg/m3. What is the total buoyant foce on the sphere

Answer 1

B_total = 1694 N , T = - 937.7 N

Step-by-step explanation:

This is an exercise of the Archimedes principle that establishes that the thrust of a liquid is equal to the weight of the dislodged volume

B = ρ g V_body

For this case we will assume that the weight of the body is in equilibrium with the thrust of the liquids and the tension of the rope

B₁ + B₂ - W + T = 0

suppose liquid 1 is water and liquid 2 is oil

ρ₁ g V₁ + ρ₂ g V₂ = W

for body weight let's use the definition of density

ρ = m / V

m = ρ V

we substitute

T = ρ g V - (ρ₁ g V₁ + ρ₂ g V₂)

In the problem we are told that the volume in the water is 75% and the volume in the oil is 25% of the body's volume.

T = ρ g V - g (ρ₁ 0.75 V + ρ₂ 0.25 V)

let's calculate the volumes

Body

V = 4/3 π r³

liquid 1 (water)

V₁ = 0.75 V = ¾ V

liquid 2 (oil)

V₂ = 0.25 V = ¼ V

we substitute

T = ρ g
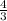`(4)/(3)` π r³ - g (ρ₁
`(3)/(4)`
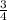
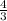`(4)/(3)` π r³ + ρ₂
`(1)/(4)`
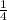
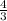`(4)/(3)` π r³)

T =
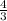`(4)/(3)` ρ g r³ - g π r³ (ρ₁ +
`(1)/(3)` ρ₂)

The term of the floating force is

B_total = g π r³ (ρ₁ +
`(1)/(3)` ρ₂)

let's calculate its value

B_total = 9.8 π 0.35³ (1000 + ⅓ 850)

B_total = 1694 N

therefore the tension in the string is

T =
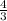`(4)/(3)` 1350 9.8 0.35³ - 1694

T = 756.3 - 1694

T = - 937.7 N

The negative sign indicates that the system tends to come out of the liquid, for which a downward force must be applied to keep it in position.