Question

An automobile assembly line operation has a scheduled mean completion time, , of minutes. The standard deviation of completion times is minutes. It is claimed that, under new management, the mean completion time has decreased. To test this claim, a random sample of completion times under new management was taken. The sample had a mean of minutes. Assume that the population is normally distributed. Can we support, at the level of significance, the claim that the mean completion time has decreased under new management

Answer 1

Explanation:

Here are the missing values;

Mean μ = 15.5 minutes

Standard deviation = 1.7 minutes

A Random sample of 90 completion

The sample mean = 15.4 minutes

Level of significance = 0.1

Then the following analysis can be made on the above study.

Firstly, the null hypothesis is
`\mathbf{H_o : \mu = 15.5}`

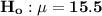
the alternative hypothesis is
`\mathbf{H_a: \mu < 15.5}`

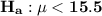
Since, the value is less than, then this is a one-tailed test.

The Z test statistics can be computed as:

`Z = ( \overline x - \mu )/((\sigma)/(√(n)) ) \ \ \sim \ \ N(0.1)`

`Z = ( 15.4-15.5 )/((1.7)/(√(90)) )`

`Z = ( -0.1 )/((1.7)/( 9.4868) )`

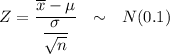
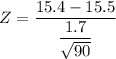
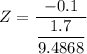
Z = −0.560

The critical value of Z at 0.1 level of significance is:

`Z_(0.1) = -1.28`

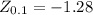
Decision Rule: We fail to reject the null hypothesis sInce -0.560 > -1.28

Conclusion: NO, there is no evidence to support the claim that the mean completion time has decreased. We conclude that the mean completion time remains at 15.5 minutes.