Question

A space probe is fired as a projectile from the Earth's surface with an initial speed of 2.05 104 m/s. What will its speed be when it is very far from the Earth

Answer 1

The value is
`v = 2.3359 *10^(4) \ m/s`

Step-by-step explanation:

From the question we are told that

The initial speed is
`u = 2.05 *10^(4) \ m/s`

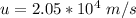
Generally the total energy possessed by the space probe when on earth is mathematically represented as

`T__(E)} = KE__(i)} + KE__(e)}`

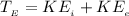
Here
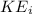`KE_i` is the kinetic energy of the space probe due to its initial speed which is mathematically represented as

`KE_i = (1)/(2) * m * u^2`

=>
`KE_i = (1)/(2) * m * (2.05 *10^(4))^2`

=>
`KE_i = 2.101 *10^(8) \ \ m \ \ J`

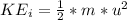
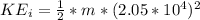
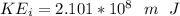
And
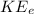`KE_e` is the kinetic energy that the space probe requires to escape the Earth's gravitational pull , this is mathematically represented as

`KE_e = (1)/(2) * m * v_e^2`

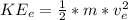
Here
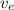`v_e` is the escape velocity from earth which has a value
`v_e = 11.2 *10^(3) \ m/s`

=>
`KE_e = (1)/(2) * m * (11.3 *10^(3))^2`

=>
`KE_e = 6.272 *10^(7) \ \ m \ \ J`

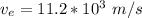
Generally given that at a position that is very far from the earth that the is Zero, the kinetic energy at that position is mathematically represented as

`KE_p = (1)/(2) * m * v^2`

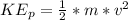
Generally from the law energy conservation we have that

`T__(E)} = KE_p`

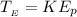
So

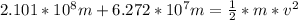
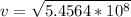
`2.101 *10^(8) m + 6.272 *10^(7) m = (1)/(2) * m * v^2`

=>
`5.4564 *10^(8) = v^2`

=>
`v = \sqrt{5.4564 *10^(8)}`

=>
`v = 2.3359 *10^(4) \ m/s`