Answer
The decision rule is
Fail to reject the null hypothesis
The conclusion is
There is no sufficient evidence to conclude that the machine is underfilling the bags
Step-by-step-explanation:
From the question we are told that
The population mean is
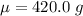
The sample size is n = 33 bags
The sample mean is
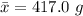
The level of significance is

The variance is
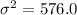
The null hypothesis is
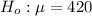
The alternative hypothesis is
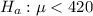
Generally the standard deviation is mathematically represented as
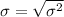
=>
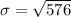
=>

Generally the test statistics is mathematically represented as
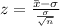
=>
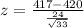
=>
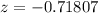
From the z table the area under the normal curve to the left corresponding to -0.71807 is

Generally looking at the values we see that
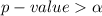 , hence
, hence
The decision rule is
Fail to reject the null hypothesis
The conclusion is
There is no sufficient evidence to conclude that the machine is underfilling the bags