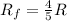Answer:
The value is
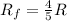
Step-by-step explanation:
From the question we are told that
The initial velocity of the proton is
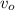
At a distance R from the nucleus the velocity is
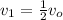
The velocity considered is
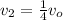
Generally considering from initial position to a position of distance R from the nucleus
Generally from the law of energy conservation we have that
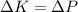
Here
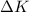 is the change in kinetic energy from initial position to a position of distance R from the nucleus , this is mathematically represented as
is the change in kinetic energy from initial position to a position of distance R from the nucleus , this is mathematically represented as
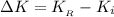
=>
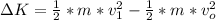
=>

=>

And
 is the change in electric potential energy from initial position to a position of distance R from the nucleus , this is mathematically represented as
is the change in electric potential energy from initial position to a position of distance R from the nucleus , this is mathematically represented as
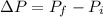
Here
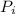 is zero because the electric potential energy at the initial stage is zero so
is zero because the electric potential energy at the initial stage is zero so

So
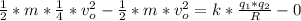
=>
![(1)/(2) * m *v_0^2 [ (1)/(4) -1 ] = k * (q_1 * q_2 )/(R)](https://img.qammunity.org/2021/formulas/physics/college/mu76zwadujtxzo0rvvc66bl88jn5g1vno8.png)
=>
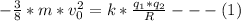
Generally considering from initial position to a position of distance
 from the nucleus
from the nucleus
Here
 represented the distance of the proton from the nucleus where the velocity is
represented the distance of the proton from the nucleus where the velocity is
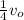
Generally from the law of energy conservation we have that
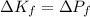
Here
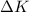 is the change in kinetic energy from initial position to a position of distance R from the nucleus , this is mathematically represented as
is the change in kinetic energy from initial position to a position of distance R from the nucleus , this is mathematically represented as
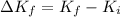
=>
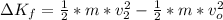
=>
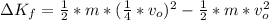
=>
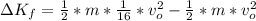
And
 is the change in electric potential energy from initial position to a position of distance
is the change in electric potential energy from initial position to a position of distance
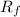 from the nucleus , this is mathematically represented as
from the nucleus , this is mathematically represented as
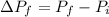
Here
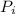 is zero because the electric potential energy at the initial stage is zero so
is zero because the electric potential energy at the initial stage is zero so

So
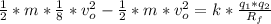
=>
![(1)/(2) * m *v_o^2 [-(15)/(16) ] = k * (q_1 * q_2 )/(R_f )](https://img.qammunity.org/2021/formulas/physics/college/14akyoopdjue7yzcgz0ns7i5b2m22jyrz4.png)
=>
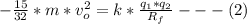
Divide equation 2 by equation 1
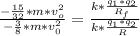
=>
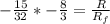
=>
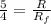
=>