Question

Suppose that scores on a particular test are normally distributed with a mean of 110 and a standard deviation of 20. What is the minimum score needed to be in the top 2% of the scores on the test

Answer 1

The minimum score needed to be in the top 2% of the scores on the test

is n = 10,00,000

Explanation:

Step(i):-

Mean of the Population = 110

Standard deviation of the Population = 20

The estimated error = 2% = 0.02

Step(ii):-

The estimated error is determined by

`E = (S.D)/(√(n) )`

`0.02 = (20)/(√(n) )`

⇒
`√(n) = (20)/(0.02) = 1000`

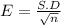
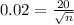
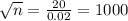
Squaring on both sides, we get

n = 10,00,000

The minimum score needed to be in the top 2% of the scores on the test

is n = 10,00,000