Question

A long-jumper leaves the ground at an angle of 20.0° above the horizontal and at a speed of 11.0 m/s.How far does he jump in the horizontal direction?(Assume his motion is equivalent to that of a particle.).

a. 12m
b. 7.94m
c. 10m
d. 0.384m​

Answer 1

The correct option is;

b. 7.94 m

Step-by-step explanation:

The given parameters of the jump of the long jumper are;

The angle above the horizontal with which the long jumper leaves the ground, θ = 20.0°

The speed with which the long jumper leaves the ground, u = 11.0 m/s

The furthest horizontal distance the long jumper jumps, given that the motion is equivalent to that of a particle, is given by the formula for the range, R, of a projectile motion as follows;

`R = (u^2 * sin \left (2 \cdot \theta \right ))/(g)`

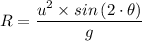
Where;

g = The acceleration due to gravity ≈ 9.8 m/s²

u = The initial velocity of the long-jumper = 11.0 m/s

θ = The angle of the direction above the horizontal the long-jumper jumps = 20.0°

Plugging in the values, gives;

`R = ((11.0 \ m/s)^2 * sin \left (2 * 20.0 ^(\circ) \right ))/(9.8) = (121 \ m^2/s^2 * sin \left (40.0 ^(\circ) \right ))/(9.8 \ m/s^2) \approx 7.94 \ m`

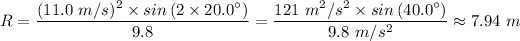
How far the long-jumper goes = The range, R, of the projectile motion ≈ 7.94 m.