Answer:
The equation of the parabola in standard is
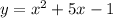
Explanation:
The standard form equation of the parabola is:

Using the three points we can find a, b and c.
Let's put the first point (0,-1)into the standard form equation.
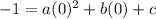
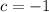
Using the second point (1,5) and the value of c found above.

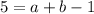
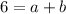 (1)
(1)
Finally using the las point (-1,-5)

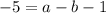
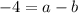 (2)
(2)
Solving the system of equations (1) and (2) we can find a and b.
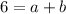
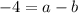
Adding both of them we have:
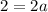
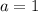
And b = 5.
Therefore, the equation of the parabola in standard form will be.
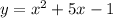
I hope it helps you!