Given :
Salt is poured from a container at 10 cm³ s-¹ and it formed a conical pile whose height at any time is 1/5 the radius of the above.
To Find :
At what rate is the height of the cone increasing when the height is 2 cm form the base of the cone.
Solution :
We know, volume of a cone is given by :
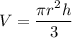
Also, h = r/5
r = 5h
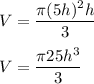
Differentiating above equation w.r.t h, we get :
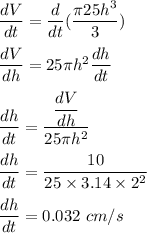
Hence, this is the required solution.