Question

Salt is poured from a container at 10 cm³ s-¹ and it formed a conical pile whose height at any time is 1/5 the radius of the above. At what rate is the height of the cone increasing when the height is 2 cm form the base of the cone?​

Answer 1

`\displaystyle (dh)/(dt) = (1)/(10 \pi)`

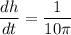
Step-by-step explanation:

Volume of a cone:

• 
  `\displaystyle V=(1)/(3) \pi r^2 h`

We have
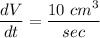`\displaystyle (dV)/(dt) = (10 \ cm^3)/(sec)` and we want to find
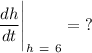`\displaystyle (dh)/(dt) \Biggr | _(h\ =\ 6)= \ ?` when the height is 2 cm.

We can see in our equation for the volume of a cone that we have three variables: V, r, and h.

Since we only have dV/dt and dh/dt, we can rewrite the equation in terms of h only.

We are given that the height of the cone is 1/5 the radius at any given time, 1/5r, so we can write this as r = 5h.

Plug this value for r into the volume formula:

• 
  `\displaystyle V =(1)/(3) \pi (5h)^2 h`
• 
  `\displaystyle V =(1)/(3) \pi \ 25h^3`

Differentiate this equation with respect to time t.

• 
  `\displaystyle (dV)/(dt) =(25)/(3) \pi \ 3h^2 \ (dh)/(dt)`
• 
  `\displaystyle (dV)/(dt) =25 \pi h^2 \ (dh)/(dt)`

Plug known values into the equation and solve for dh/dt.

• 
  `\displaystyle 10 = 25 \pi (2)^2 \ (dh)/(dt)`
• 
  `\displaystyle 10 = 100 \pi \ (dh)/(dt)`

Divide both sides by 100π to solve for dh/dt.

• 
  `\displaystyle (10)/(100 \pi) = (dh)/(dt)`
• 
  `\displaystyle (dh)/(dt) = (1)/(10 \pi)`

The height of the cone is increasing at a rate of 1/10π cm per second.