Question

A horizontal disc of radius 45 cm rotates about a vertical axis through its centre. The disc makes one full

revolution in 1.40 s. A particle of mass 0.054 kg is placed at a distance of 22 cm from the centre of the disc.
The particle does not move relative to the disc.
a On a copy of the diagram draw arrows to represent the velocity and acceleration of the particle. [2]
b Calculate the angular speed and the linear speed of the particle. [2]
c The coe cient of static friction between the disc and the particle is 0.82. Determine the largest distance
from the centre of the disc where the particle can be placed and still not move relative to the disc. [3]
d The particle is to remain at its original distance of 22cm from the centre of the disc.
i Determine the maximum angular speed of the disc so that the particle does not move relative to
the disc. [2]
ii The disc now begins to rotate at an angular speed that is greater than the answer in d i. Describe
qualitatively what happens to the particle. [2]

Answer 1

a. Please find attached the diagram of the disc, having arrows that represent the velocity and the acceleration of the particle placed on it

b. The angular speed is approximately 4.488 rad/s

The linear speed is approximately 0.987 m/s

c. The largest distance from the center of the disc where the particle can be placed and still not move is approximately 0.399 m from the center of the disc

d. i The maximum angular speed of the disk so that the particle does not move relative to the disk is approximately 6.044 rad/sec

ii When the angular speed with which the disc rotates is more than the the answer of question d i above, the particle slips on the disc, and the disc begins to rotate faster than the particle, while the particle is swung in an outward radial direction off the disc due to the centrifugal forces

Step-by-step explanation:

The given parameters are;

The radius of the horizontal disc, r = 45 cm = 0.45 m

The time the disc makes one full revolution, T = 1.40 s

The mass of the particle placed on the disc = 0.054 kg

The location on the disc the particle is placed = 22 cm from the disc's center

a. Please find attached the diagram of the disc created with Microsoft Visio, with arrows representing the velocity and the acceleration of the particle placed on the disk

b. The angular speed, ω = 2·π/T = 2 × π/1.4 ≈ 4.488 rad/s

The linear speed, v = ω × r = 4.488 rad/s × 0.22 m ≈ 0.987 m/s

The linear speed, v ≈ 0.987 m/s

c. The given coefficient of static friction = 0.82

Therefore;

The frictional force that prevents motion = Weight of the particle × The coefficient of static friction

The frictional force that prevents motion is
`F_f` = 0.054 × 9.8 × 0.82 ≈ 0.434 N

`F_f` ≈ 0.434 N

Therefore, for the largest distance from the center of the disc where the particle can be placed and still not move, r, is given by the formula for the centripetal force,
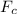`F_c`, acting on the particle as follows;

For static equilibrium, no movement of the particle relative to the disc, we have;

`F_f` =
`F_c`

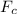
Where;

`F_c = (m * v^2)/(r) = m * \omega ^2 * r`

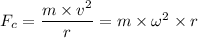
Which gives;

`F_c = {0.054 \ kg * (4.488 \ rad/s)^2} * r = F_f = 0.434 \ N`

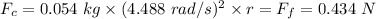
r = 0.434 N/(0.054 kg × (4.488 rad/s)²) ≈ 0.399 m

The largest distance from the center of the disc where the particle can be placed and still not move, r = 0.399 m from the center of the disc

d. i From the static equilibrium equation where r = 0.22 m, we have;

`F_c = {0.054 \ kg * \omega ^2} * 0.22 \ m = F_f = 0.434 \ N`

ω = √(0.434 N/(0.054 kg × (0.22 m))) ≈ 6.044 rad/sec

The maximum angular speed of the disk so that the particle does not move relative to the disk, ω ≈ 6.044 rad/sec

ii When the angular speed with which the disc rotates is more than the the answer of question d i above, we have

The particle begins to slip on the disc such that the disc rotates faster than the particle and the particle tends to rotate slower than the speed pf the disc and is swung off the disc by centripetal force acting on the particle due to the rotational motion of the disc.