Question

The figure below shows a large rectangle with a small rectangle cut out of it.

What is the area?

Answer 1

40

Explanation:

We can make a big square by making a line at the top open edge (as shown in the image attached below). We will first solve for
`A_(2)` and then
`A_(1)`, and then finally solving for out answer by subtracting
`A_(1)` from
`A_(2)` .

`A_(2)` is a square with side lengths of 7, so the area is 7 * 7 = 49.

`A_(1)` is a smaller square with side lengths of 3, so the area is 3 * 3 = 9.

`A_(2) - A_(1) = 49 - 9 = 40`

∴ Our final answer is 40

Answer 2

40 square units

Explanation:

The question gives that both the large shape and the small missing shape are rectangles. The formula for the area of a rectangle is
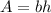`A=bh` where "A" is the "Area", "b" is the "base" (bottom edge), and "h" is the height (side edge).

For rectangles, opposite sides (example: top & bottom) have the same length, so the top of the missing rectangle must also be 3.

To find the area of the figure, we must find the difference (subtraction) between the large rectangle (without a hole out of it) and the rectangular hole.

`A_{\text{figure}}=A_{\text{large rectangle without hole}}-A_{\text{hole}}\\A_{\text{figure}}=(7)(7)-(3)(3)\\A_{\text{figure}}=49-9\\A_{\text{figure}}=40`

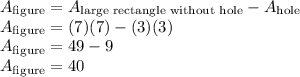
So, the area of the figure is 40 square units.