Question

Dec 23, 8:45:08 PM

Find three consecutive POSITIVE ODD integers such that when you multiply the first
and third the result is nine less than six times the second integer.

Answer 1

3, 5, 7

Explanation:

Let the first of the three positive consecutive odd numbers be
`x`.

Now, the second odd number =
`x+2\\`

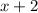
And, the third odd number =
`x+4`

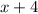
As per question statement, the multiplication of the first and third odd number is 9 lesser than the 6 times the second integer.

Writing the equation, we get:

`x(x+4) = 6(x+2)-9\\\Rightarrow x^(2) +4x=6x+12-9\\\Rightarrow x^(2) +4x-6x = 3\\\Rightarrow x^(2) -2x - 3=0\\\text{Solving the above equation by factorization method:}\\\Rightarrow x^(2) -3x +x - 3=0\\\Rightarrow x(x -3) + 1(x - 3)=0\\\Rightarrow (x -3) (x+ 1)=0\\\Rightarrow x =3, -1`

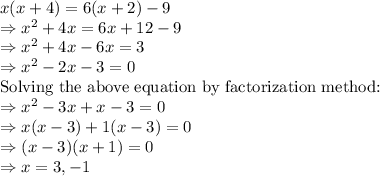
As, we got a quadratic equation, so we have two solutions here.

One is positive integer and other one is negative.

So, solution is
`x=3`

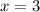
First number is 3.

Second number is 3 + 2 = 5

Third number is 5 + 2 = 7