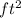Answer:
Maximum Ares architect can build is 36,450
Step-by-step explanation:
Suppose
The Perpendicular of the triangle = l
The Base of the triangle = b
The hypotenuse of the triangle = h
The hypotenuse of the triangle can be calculated as follow
h =
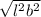
Total Budget = $1,620
As the architect does not want to build anything on the hypotenuse of the triangle area.
So as per given condition
( $9 x l ) + ( $3 x b ) = $1,620
$3 ( 3l + b ) = $1,620
3l + b = $1,620 / $3
3l + b = 540
b = 540 - 3l ...........(1)
Area = 1/2 x l x b
using (1) we will have
Area = 1/2 x l x ($540 - 3l)
Now differentiating w.r.t l
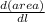 =
=
![((1)/(2) [ 540l - 3l^(2)] )/(dl)](https://img.qammunity.org/2021/formulas/business/college/1hg9kbnfbd49vc8wkcfzuqw3ohyx4dgcwl.png)
0 =
![(1)/(2) [ 540 - 6l] }](https://img.qammunity.org/2021/formulas/business/college/dn656r2dsef7ohvfr7z04qi8msmkwszlsi.png)
0 = 540 - 6l
6l = 540
l = 540/6
l = 90 ft
Placing value of l in (1)
b = 540 - 3(90)
b = 540 - 270
b = 270
So, Maximum area will be calculated as follow
Maximum Ares =
 x 270 x 270
x 270 x 270
Maximum Ares = 36,450