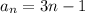Question

Write an equation for the nth term of the arithmetic sequence.
2, 5, 8, 11, ...

Answer 1

An equation for the nth term of the arithmetic sequence.

`a_n=3n-1`

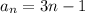
Explanation:

Given the sequence

2,5,8,11,...

An arithmetic sequence has a constant difference 'd' and is defined by

`a_n=a_1+\left(n-1\right)d`

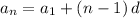
here

• a₁ = 2

computing the differences of all the adjacent terms

• d = 5-2 = 3, d = 8-5=3, d=11-8=3

Using the nth term formula

`a_n=a_1+\left(n-1\right)d`

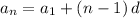
substituting a₁ = 2, d = 3

`a_n=2+\left(n-1\right)3`

`=2+3n-3`

`=3n-1`

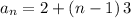
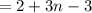
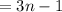
Thus, an equation for the nth term of the arithmetic sequence.

`a_n=3n-1`